7.4 B 树和 B+ 树
7.4.1 B 树及其基本操作
B 树是所有结点平衡因子均等于 0 的多路平衡查找树。
B 树的所有结点的孩子个数的最大值称为 B 树的阶。
| m 阶 B 树结点 | 子树个数 | 关键字个数 |
|---|---|---|
| 根结点 | $(2,m)$ | $(1,m-1)$ |
| 除根结点外所有非叶结点 | $(\left\lceil m/2\right\rceil ,m)$ | $(\left\lceil m/2\right\rceil-1 ,m-1)$ |
m 阶 B 树
- 每个结点最多有 m 颗子树,最多有 m-1 个关键字。
- 根结点至少两颗子树。
- 非叶结点至少有$\left\lceil m/2\right\rceil$颗子树,至少有$\left\lceil m/2\right\rceil$-1 个关键字。
- 查找树。
- 叶结点在同一层,代表查找失败的位置。
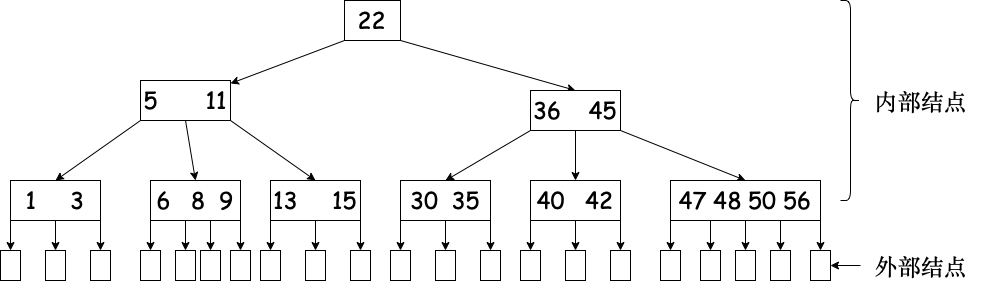
1.B 树的高度(磁盘存取次数)
2.B 树的查找
B 树的查找包括两个操作:
1、在 B 树中找结点。
2、在结点内找关键字。
由于 B 树常存储在磁盘上,因此前一个查找操作是在磁盘上进行的,而后一个查找操作是在内存中进行的。
3.B 树的插入
(1)定位
找到最底层非叶结点的插入位置。
(2)插入
插入后检查被插入节点内关键字的个数,当插入后结点关键字个数大于 m-1 时,必须对结点进行分裂。
分裂方法:左部分包含的关键字放在原结点中,右部分包含的关键字放在新结点中,中间位置 ($\left\lceil m/2\right\rceil$) 的结点插入原结点的父结点。
4.B 树的删除 (删除关键字,结点不会删除)
被删除结点不在终端结点时,用 k 的前驱或后继替换,转换为删除终端结点。
- 直接删除关键字。当被删除关键字所在结点关键字个数$\geqslant \left\lceil m/2\right\rceil$ 。
- 兄弟够借。兄弟变父亲,父亲变自己。
- 兄弟不够借。兄弟、父亲、自己合并。
7.4.2 B+ 树
每个分支结点最多有 m 棵子树。
非叶根结点至少有两颗子树,其他分支结点至少有$\left\lceil m/2\right\rceil$颗子树。
结点的子树个数和关键字个数相等。
所有叶结点包含全部关键字,按大小顺序排列,相邻叶结点按大小顺序相互链接起来。
所有分支结点包含它的各个子结点的关键字最大值和指针。
n 阶 B+ 树结点 子树个数/关键字个数 根结点 $(2,m)$ 除根结点外所有非叶结点 $(\left\lceil m/2\right\rceil ,m)$
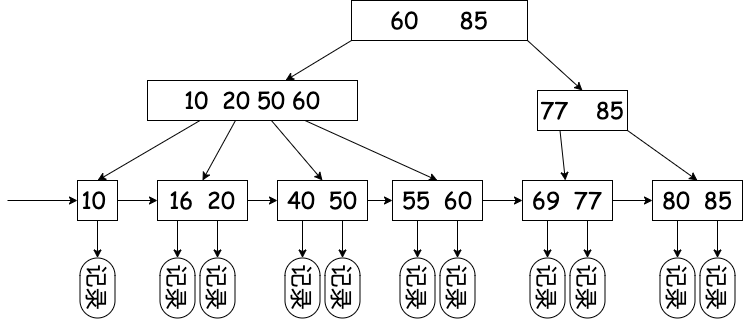
B+ 树所有叶结点包含全部关键字信息,因此可以顺序查找,B 树不支持顺序查找。
