6.4 图的应用
6.4.1 最小生成树
1.Prim 算法
每次将代价最小的新顶点纳入生成树,直到所有顶点都纳入为止。
时间复杂度 $O(v^2)$
2.Kruskal 算法
每次选择一条权值最小的边连通,直到所有结点连通。
时间复杂度 $O(|E|log|E|)$
6.4.2 最短路径
Dijkstra 算法求单源最短路径
迭代,每次求出一个最短路径
不适用于负权值带权图
求源点 a 到其他各顶点的最短路径?
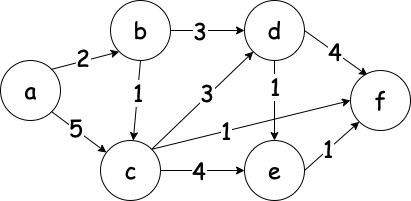
| b | c | d | e | f |
|---|---|---|---|---|
| 2 | 5 | ∞ | ∞ | ∞ |
| 2 | 3 | 5 | ∞ | ∞ |
| 2 | 3 | 5 | 6 | 4 |
| 2 | 3 | 5 | 6 | 4 |
| 2 | 3 | 5 | 6 | 4 |
| 2 | 3 | 5 | 6 | 4 |
Floyd 算法求各顶点之间的最短路径问题
允许 1 个结点中转
允许 2 个结点中转
。。
允许所有结点中转
6.4.3 有向无环图描述表达式
DAG 图:有向无环图
6.4.4 拓扑排序
AOV 网:DAG 图表示工程,顶点表示活动。
6.4.5 关键路径
从源点到汇点的所有路径当中,具有最大路径长度的路径称为关键路径。
AOE 网:边表示活动
事件的最早发生时间 ve(k)
从源点 $v_{1}$ 到顶点 $v_{k}$ 的最长路径长度。
万事具备,只欠东风
$ve(源点)=0$
$ve(k)=Max{ve(j)+Weight(v_{j},v_{k})}$
事件的最迟发生时间 vl(k)
结束时间 - 所需时间=最晚开始时间
$vl(汇点)=ve(汇点)$
$vl(k)=Min{vl(j)-Weight(v_{k},v_{j})}$
活动 $a_{i}$ 的最早开始时间 e(i)
$e(i)=ve(i)$
活动 $a_{i}$ 的最迟开始时间 l(i)
$l(i)=vl(i)-Weight(v_{k},v_{j})$
活动 $a_{i}$ 的时间差额 d(i)=l(i)-e(i)
在不增加整个工程所需总时间的情况下,活动 $a_{i}$ 可以拖延的时间。
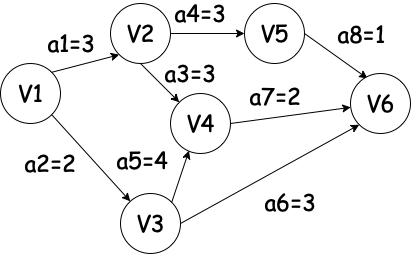
| V1 | V2 | V3 | V4 | V5 | V6 | |
|---|---|---|---|---|---|---|
| ve(i) | 0 | 3 | 2 | 6 | 6 | 8 |
| vl(i) | 0 | 4 | 2 | 6 | 7 | 8 |
| a1 | a2 | a3 | a4 | a5 | a6 | a7 | a8 | |
|---|---|---|---|---|---|---|---|---|
| e(i) | 0 | 0 | 3 | 3 | 2 | 2 | 6 | 6 |
| l(i) | 1 | 0 | 4 | 4 | 2 | 5 | 6 | 7 |
| l(i)-e(i) | 1 | 0 | 1 | 1 | 0 | 3 | 0 | 1 |
