7.3 树型查找
7.3.1 二叉排序树 (BST)
构造二叉排序树目的:提高查找、插入和删除关键字的速度。
1.二叉排序树的定义
二叉排序树或者是一颗空树,或者是具有下列特性的二叉树:
(1)若左子树非空,则左子树上所有结点的值均小于根结点的值。
(2)若右子树非空,则右子树上所有结点的值均大于根结点的值。
(3)左、右子树也分别是一颗二叉排序树。
LeetCode[109] 有序链表转换二叉搜索树
class Solution
{
public:
ListNode *findMidNode(ListNode *left, ListNode *right)
{
ListNode *slow = left;
ListNode *fast = left;
while (fast != right && fast->next != right)
{
slow = slow->next;
fast = fast->next->next;
}
return slow;
}
TreeNode *buildBST(ListNode *left, ListNode *right)
{
if (left == right)
{
return nullptr;
}
ListNode *mid = findMidNode(left, right);
TreeNode *root = new TreeNode(mid->val);
root->left = buildBST(left, mid);
root->right = buildBST(mid->next, right);
return root;
}
TreeNode *sortedListToBST(ListNode *head)
{
return buildBST(head, nullptr);
}
};
7.3.2 平衡二叉树
任意节点左右子树高度差绝对值不超过 1。
构成平衡二叉树最少结点数递推公式 $n_{0}=0,n_{1}=1,n_{2}=2,n_{h}=1+n_{h-1}+n_{h-2}$,
插入
LL(右单旋转)、
RR(左单旋转)、
LR(先左后右双旋转):在 A 的左孩子的右子树上插入新结点
RL(先右后左双旋转):在 A 的右孩子的左子树上插入新结点
平衡因子为 2 和 1 的结点重新排列,再把其他结点接上去。
删除
向上回溯,找到第一个不平衡的节点,进行调整
7.3.3 红黑树
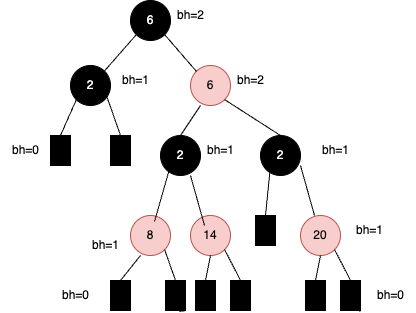
为什么要有红黑树?
因为平衡二叉树的要求太严格,导致每次进行插入/删除结点时,几乎都会破坏平衡二叉树。在频繁插入/删除结点的场景中,性能会大幅度下降。所以有了红黑树。
左右高度不超过两倍
红黑树是二叉排序树
- 每个结点是红色或黑色
- 根结点是黑色的
- 叶结点(NULL 结点)都是黑色的
- 红结点的父结点和孩子结点都是黑色的
- 每个结点,从该结点到任一叶结点的简单路径上,所含黑结点的数量相同。记为黑高,根结点的黑高记为红黑树的黑高。
“左根右,根叶黑,不红红,黑路同”
插入
新插入红黑树的结点 z 初始为红色。如果 z 是根结点就是黑色。
违反“不红红”的:
黑叔:
- LR:左旋 + 右旋,儿换爷 + 染色
- LL:右单旋,父换爷 + 染色
- RR:左单选,父换爷 + 染色
- RL:右旋 + 左旋,儿换爷 + 染色
红叔:
叔父爷染色 + 爷变新
删除
时间复杂度$O\left( \log_{2} n\right)$
#include <iostream>
using namespace std;
enum Color {
RED, BLACK
};
struct Node {
int key;
Color color;
Node *left;
Node *right;
Node(int k) : key(k), color(RED), left(nullptr), right(nullptr) {}
};
class RedBlackTree {
public:
RedBlackTree() : root(nullptr) {}
void insert(int key);
bool find(int key);
private:
void insert(Node *&node, int key);
bool find(Node *node, int key);
void rotate_left(Node *&node);
void rotate_right(Node *&node);
void flip_colors(Node *&node);
Node *root;
};
void RedBlackTree::insert(int key) {
insert(root, key);
root->color = BLACK; // 根节点始终为黑色
}
void RedBlackTree::insert(Node *&node, int key) {
if (node == nullptr) {
node = new Node(key);
return;
}
if (key < node->key) { insert(node->left, key); }
else if (key > node->key) { insert(node->right, key); }
else {
return; // 已存在该键值,不插入
}
// 红黑树自平衡
if (node->right && node->right->color == RED && (!node->left || node->left->color == BLACK)) {
rotate_left(node);
}
if (node->left && node->left->color == RED && node->left->left && node->left->left->color == RED) {
rotate_right(node);
}
if (node->left && node->left->color == RED && node->right && node->right->color == RED) {
flip_colors(node);
}
}
bool RedBlackTree::find(int key) { return find(root, key); }
bool RedBlackTree::find(Node *node, int key) {
if (node == nullptr) { return false; }
if (key < node->key) { return find(node->left, key); }
else if (key > node->key) {
return find(node->right, key);
} else { return true; }
}
void RedBlackTree::rotate_left(Node *&node) {
Node *tmp = node->right;
node->right = tmp->left;
tmp->left = node;
tmp->color = node->color;
node->color = RED;
node = tmp;
}
void RedBlackTree::rotate_right(Node *&node) {
Node *tmp = node->left;
node->left = tmp->right;
tmp->right = node;
tmp->color = node->color;
node->color = RED;
node = tmp;
}
void RedBlackTree::flip_colors(Node *&node) {
node->color = RED;
node->left->color = BLACK;
node->right->color = BLACK;
}
int main() {
RedBlackTree tree;
tree.insert(5);
tree.insert(2);
tree.insert(8);
tree.insert(1);
tree.insert(4);
tree.insert(7);
tree.insert(9);
tree.insert(3);
tree.insert(6);
cout << "Find 5: " << tree.find(5) << endl; // 输出 1
cout << "Find 10: " << tree.find(10) << endl; // 输出 0
return 0;
}
